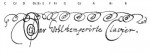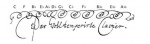The term “well-tempered clavier” obviously refers to keyboard temperament. At the core of any discussion of temperament lies a mysterious acoustic phenomenon, which was discovered by Pythagoras in the sixth century B.C.: When a string is divided in half, the interval between the pitch of the full string and the pitch of its half-length is a pure octave; when a string is divided in the ratio 3:2, the interval between the pitch of the full string and the pitch of its two-thirds is a pure fifth.

As we know, a circle of 12 fifths begins and ends with the same note. Strangely, however, 12 pure fifths do not really “fit” within the octave, but actually exceed the octave, so that the final pitch is slightly different from the original one (it is lower than the original if the circle goes down, and higher if the circle goes up). The amount by which 12 fifths exceed the octave is called the “Pythagorean comma.” Therefore, to put it simply, temperament is the method of “compromising” the purity of the fifths in order to keep the octave pure. (Figure 1)

In practice, singers and most instrumentalists solve the problem spontaneously by intuitively adjusting their intonation. But this cannot be done on instruments of fixed pitch, like harpsichord, piano, organ, harp, lute, or guitar. These instruments require a choice of temperament, which dictates the degree of “falseness” of the intervals, and therefore the “usability” of the various keys. (If one of the fifths is very false, the keys that include this fifth will be unplayable.)

The standard temperament nowadays is “equal temperament,” in which all 12 fifths are narrowed by the same amount (1/12th of the Pythagorean comma). In this temperament (which is used in all modern pianos, for example), all the keys are equally false, but the degree of their “falseness” is relatively small. However, “equal temperament” did not become the standard until late in the 18th century or later (and well after Bach’s death). Until then, a large variety of non-equal temperament systems were used, and it is probably to one of these systems that Bach referred in the title of his 1722 collection.

The terms “well-tempered” and “well-temperament” were first coined in 1691 by German theorist Andreas Werckmeister, referring to a sort of temperament in which the fifths are of different sizes, but none of the fifths is too false to use. In “well-temperament,” all the keys are playable, yet they vary in their purity and timbre. The concept of variety was an important part of Baroque aesthetics, and the different colors of the various keys (created by non-equal temperament) was considered an advantage. Perhaps this is what Bach meant to demonstrate in his collection of preludes and fugues. While Werckmeister gives clear instructions for his proposed temperament, there is no direct evidence of the exact kind of temperament that Bach himself used.

Over the years, attempts to reconstruct Bach’s temperament were made by a number of musicologists, from Kirnberger and Marpurg in the 18th century to 20th-century musicologists Herbert Kellner and John Barnes. But perhaps the most curious and unusual approach to the question of Bach’s temperament was presented in the February and May 2005 issues of Early Music by harpsichordist/mathematician Bradley Lehman. (The illustrations in Figures 2-5 in this article appeared in that publication.)

Examining the title page of the W.T.C. from 1722, Lehman noticed that the decorative scroll above the text features 11 loops of three different kinds (simple, double, and convoluted). (Figure 2) It occurred to him that 11 is the number that would describe the temperament of 12 fifths (if the first note is given, it would also be the last note of the circle, rendering the “12th loop” unnecessary). He noticed the letter C attached to the first loop from the right, and then decided to turn the loops upside down. (Figure 3)

Lehman states that in the Baroque period the normal amount of tempering a fifth is 1/6th of a Pythagorean comma, which, he believes, is represented in the squiggle by the convoluted spiral. He interprets the double-spiraled loops to represent the tempering of 1/12th of a Pythagorean comma, and the simple loops to indicate pure fifths. He then devises a temperament he believes to be the one used by Bach, and which, according to Lehman, brings out qualities of Bach’s composition that are hidden in equal temperament.

Lehman’s theory received tremendous attention, being highly praised by some and severely criticized by others. The November 2006 issue of Early Music featured several responses to Lehman’s article on Bach’s temperament. One of them, written by John O’Donnell, challenges Lehman’s interpretation and offers an interesting alternative for the reading of the title-page scroll.

O’Donnell claims that, although tuning is done with fifths, its customary notation in the Baroque period was actually chromatic, rising from C. This is also the order chosen by Bach for the 24 preludes and fugues. Examining the scroll of the Well-Tempered title page once again, O’Donnell notices that the “D” of Das intersects with the third loop and that, to its left, there is a squiggle that looks like “Es,” the German notation for E flat, while to its right appears the German tablature symbol of “Dis” (D sharp). O’Donnell mentions the E-flat/D-sharp Prelude and Fugue, which, curiously, is the only piece in the collection that refers directly to the enharmonic phenomenon.

O’Donnell assigns pitch names to the scroll, starting from C on the left and ascending chromatically until reaching B on the right side. (Figure 4)

Based on his reading of the scroll, O’Donnell constructs a temperament system which, according to him, represents Bach’s own.

In 2007, in response to these articles, musicologist John Francis posted an article on the Internet that offered a systematic analysis of the scroll, considering the diagram’s orientation (left to right; right to left), tuning direction, starting position, and degree of temperament, so that, in total, 144 possibilities were mathematically analyzed. Francis compared his results with 52 existing tuning systems, and finally came up with a reading of the scroll, as seen in Figure 5.

However, with all of this said and done, to this day no one knows what Bach’s temperament really was. Whether the decorative scroll of the Well-Tempered Clavier is indeed a temperament prescription or not, it now provides a subject for endless interpretation, almost like the music that follows the title page. The quest for Bach’s temperament will most likely continue to preoccupy musicians and theorists for generations to come.